Pythonで学ぶ統計学(5): 同時確率分布 - 投資のためのデータサイエンス

データ解析の実務で複数のデータを扱うことは頻繁にあります。例えば気温とアイスクリームの売上高の関係を分析したい場合は、この２つの項目に対応する２つの確率変数の「同時確率分布」を考えます。

連続量の場合、２つの確率変数 $X,Y$ と定数 $a,b,c,d$ について、同時確率密度関数は以下の式を満たすものとして与えられます。

$\displaystyle P(a\leq X\leq b,c\leq Y\leq d)=\int_{a}^{b}\int_{c}^{d}f_{XY}(x,y)dxdy$

多変数の同時確率分布は、条件付き確率や変数変換などの基礎となるので非常に重要です。

連続分布で最も基本的な正規分布についての多次元版を考えます。p次元の確率変数ベクトル $X$ が平均ベクトル $\mu$ 、分散共分散行列（正定値の行列） $\Sigma$ の多次元正規分布にしたがうとすると、その確率密度関数（スカラー量）は以下の式で表されます。

$\displaystyle f(x;\mu ,\Sigma )=\frac{1}{(2\pi )^{p/2}|\Sigma |^{1/2}}\exp \left \{ -\frac{1}{2}(x-\mu )'\Sigma ^{-1}(x-\mu )\right \}$

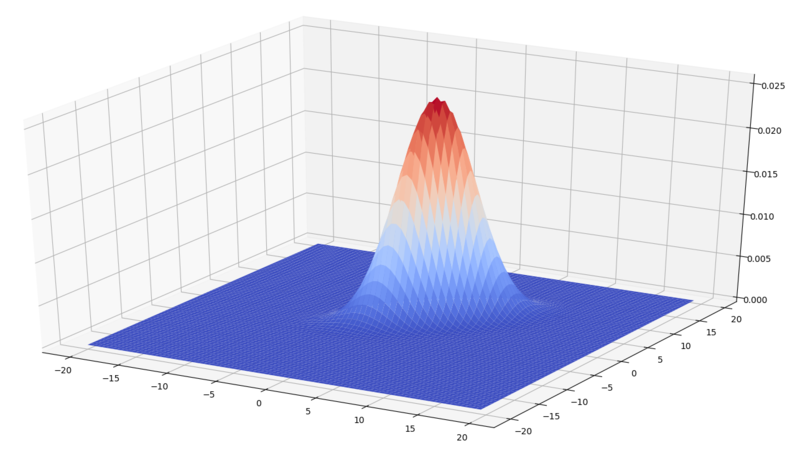
以下のpythonコードは、2次元正規分布の確率密度関数の山を3D図面に描くもので、Qiitaサイトより引用したものです。このコードのキーポイントは、まずnp.meshgrid()関数によって描こうとする(x,y)座標軸の組を生成し、そのペアをravelメソッドによりを一列にリストとして並べる。次に内部で定義したgaussian()関数はその値のペアから確率密度関数の値を直接式を書いて求めていますが、二次形式の部分は（ペアのリスト）×（行列）×（ペアのリストの転置）の対角成分をとればいいこと。さらに計算結果をreshapeメソッドで元の格子データ行列の形に戻した上で描画をしています。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
# メッシュグリッドデータの生成
x = np.arange(-20, 20, 0.5)
y = np.arange(-20, 20, 0.5)
X, Y = np.meshgrid(x, y)
z = np.c_[X.ravel(),Y.ravel()]
# 確率密度関数の値の計算関数
def gaussian(x,mu,sigma):
    det = np.linalg.det(sigma)
    inv = np.linalg.inv(sigma)
    n = x.ndim
    return np.exp(-np.diag((x - mu)@inv@(x - mu).T)/2.0) / (np.sqrt((2 * np.pi) ** n * det))
# パラメータを指定して確率密度を計算
mu = np.array([2,3])
sigma = np.array([[8,5],[5,8]])
Z = gaussian(z,mu,sigma)
shape = X.shape
Z = Z.reshape(shape)
# 三次元グラフに描画
fig = plt.figure(figsize = (15, 15))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
plt.show()