(2024/8/7) yfinanceライブラリの新しいバージョンに対応してコードを修正しました。
今回もAI絡みの内容です。最近あるセミナーで、DTW(動的時間伸縮法)を用いた株価予測について話があったので、この分野について少し調べました。
今回紹介するコードはmediumの英文記事からの引用です。
DTWは時系列データのパターンとしての類似度を評価するもので、音声認識などに用いられています。類似度を評価するデータの長さは必ずしも揃っている必要はありません。
以下のコードはデータ獲得部分を除いてはほぼオリジナル記事のままで、当方で日本語の注釈をつけています。
まずライブラリをインポートします。
# ライブラリのインポート import yfinance as yf import pandas as pd import numpy as np import matplotlib.pyplot as plt from fastdtw import fastdtw from scipy.spatial.distance import euclidean from datetime import date, datetime, timedelta
次に関数を定義します
def normalize(ts): return (ts - ts.min()) / (ts.max() - ts.min()) # 最小値0, 最大値1で標準化した上でfastdtw()により非類似度を計算する def dtw_distance(ts1, ts2): ts1_normalized = normalize(ts1) ts2_normalized = normalize(ts2) distance, _ = fastdtw(ts1_normalized.reshape(-1, 1), ts2_normalized.reshape(-1, 1), dist=euclidean) return distance def find_most_similar_pattern(n_days): current_window = price_data_pct_change[-n_days:].values # 初期値として(∞,-1)からなる5つのタプルを生成 min_distances = [(float('inf'), -1) for _ in range(5)] # 全ての開始時点についてのループを5回まわすことにより距離の小さい5つのケースを抽出する for start_index in range(len(price_data_pct_change) - 2 * n_days - subsequent_days): past_window = price_data_pct_change[start_index:start_index + n_days].values distance = dtw_distance(current_window, past_window) for i, (min_distance, _) in enumerate(min_distances): if distance < min_distance: min_distances[i] = (distance, start_index) break return min_distances
次に株価データを読み込み、データの前処理とパラメータの設定を行います。
# yahooサイトからデータをダウンロード ticker = '9983.T' # 9983はファーストリテイリング end_date = datetime.today() # 分析に用いるデータ期間を指定する start_date = end_date - timedelta(days=3650) data = yf.download(ticker, start_date, end_date) # 終値を価格データとする price_data = data['Close'] # (y(t)-y(t-1))/y(t-1) の変化率データに変換する price_data_pct_change = price_data.pct_change().dropna() # 3通りの窓の期間について評価する days_to = [15, 20, 30] # 現在時点から何日先までの予測値をプロットするかを指定する subsequent_days = 20
続いて3通りの窓の期間について、直近の株価の動きに最も似ている5つのパターンを抽出し、グラフに描きます。
for n_days in days_to: min_distances = find_most_similar_pattern(n_days) fig, axs = plt.subplots(1, 2, figsize=(30, 6)) # 株価過去データの描画 axs[0].plot(price_data, color='blue', label='Overall stock price') color_cycle = ['red', 'green', 'purple', 'orange', 'cyan'] subsequent_prices = [] # 類似パターンとして抽出された部分を色を変えて再描画する for i, (_, start_index) in enumerate(min_distances): color = color_cycle[i % len(color_cycle)] past_window_start_date = price_data.index[start_index] past_window_end_date = price_data.index[start_index + n_days + subsequent_days] axs[0].plot(price_data[past_window_start_date:past_window_end_date], color=color, label=f"Pattern {i + 1}") # Store subsequent prices for median calculation subsequent_window = price_data_pct_change[start_index + n_days : start_index + n_days + subsequent_days].values subsequent_prices.append(subsequent_window) axs[0].set_title(f'{ticker} Stock Price Data') axs[0].set_xlabel('Date') axs[0].set_ylabel('Stock Price') axs[0].legend() # 類似パターンの描画:pct_change()により変換された変化率の時系列は、(各要素+1)にcumprod()を適用することにより元に戻す for i, (_, start_index) in enumerate(min_distances): color = color_cycle[i % len(color_cycle)] past_window = price_data_pct_change[start_index:start_index + n_days + subsequent_days] reindexed_past_window = (past_window + 1).cumprod() * 100 axs[1].plot(range(n_days + subsequent_days), reindexed_past_window, color=color, linewidth=3 if i == 0 else 1, label=f"Past window {i + 1} (with subsequent {subsequent_days} days)") # 実際の株価パターンを類似パターンの図に埋め込む reindexed_current_window = (price_data_pct_change[-n_days:] + 1).cumprod() * 100 axs[1].plot(range(n_days), reindexed_current_window, color='k', linewidth=3, label="Current window") # 5つの予測パターンの中央値を計算して描画する subsequent_prices = np.array(subsequent_prices) median_subsequent_prices = np.median(subsequent_prices, axis=0) median_subsequent_prices_cum = (median_subsequent_prices + 1).cumprod() * reindexed_current_window.iloc[-1] axs[1].plot(range(n_days, n_days + subsequent_days), median_subsequent_prices_cum, color='black', linestyle='dashed', label="Median Subsequent Price Estimation") axs[1].set_title(f"Most similar {n_days}-day patterns in {ticker} stock price history (aligned, reindexed)") axs[1].set_xlabel("Days") axs[1].set_ylabel("Reindexed Price") axs[1].legend() plt.show()
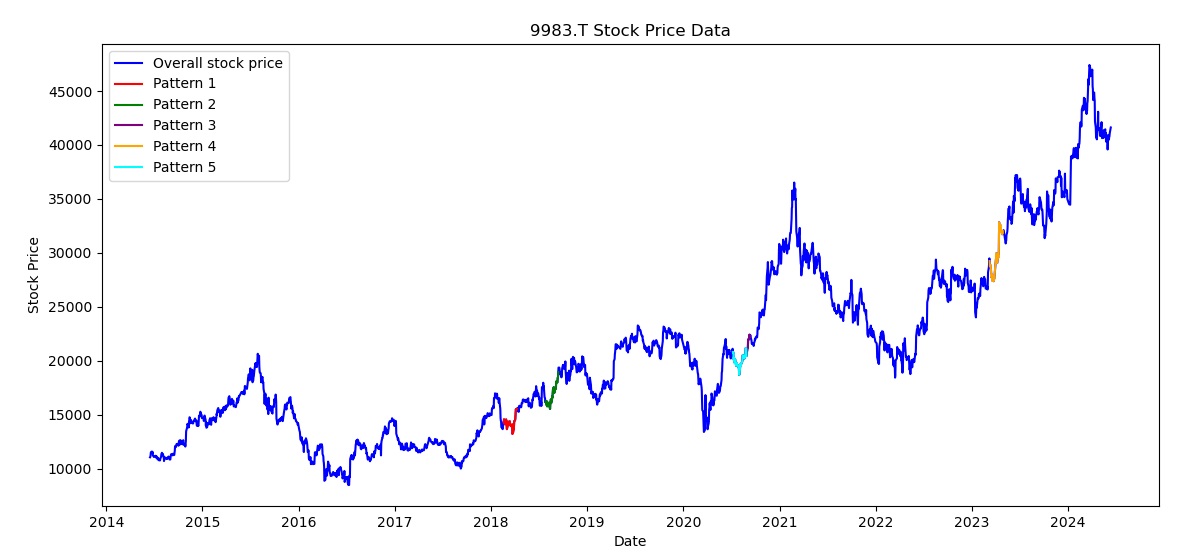

上の図は窓の期間が15日の場合の結果です。原記事ではノイズ低減・補助変数の導入・機械学習との統合・多変量DTWを今後の課題として挙げています。このDTWですが、ネット検索をしてみると、株価予測へのAIの適用の手法の一つとして検討されている事例がいくつもあります。